Sandbox

Circular restricted 3-body problem

A body of negligible mass (the “planetoid”) moves under the influence of two massive bodies. With respect to a rotating reference frame, the two co-orbiting bodies are stationary.

Equations of motion

We scale the masses of the two larger bodies to $1 − \mu$ and $\mu$ and their positions relative to the moving reference frame by the vectors $(1 - \mu) \hat{e_1}$ and $-\mu \hat{e_1}$, so that their centre of mass is at the origin of coordinates.

\[\begin{align} \dot{x_1} & = & u_1 \\ \dot{x_2} & = & u_2 \\ \dot{x_3} & = & u_3 \\ \end{align}\] \[\begin{align} \dot{u_1} & = & 2 u_2 + x_1 - \dfrac{\mu (x_1 + \mu - 1)}{\Big( x_2^2 + x_3^2 + (x_1 + \mu - 1)^2 \Big)^{\frac{3}{2}}} - \dfrac{(1 - \mu)(x_1 + \mu)}{\Big( x_2^2 + x_3^2 + (x_1 + \mu)^2 \Big)^{\frac{3}{2}}} \\ \dot{u_2} & = & -2 u_1 + x_2 - \dfrac{\mu x_2}{\Big( x_2^2 + x_3^2 + (x_1 + \mu - 1)^2 \Big)^{\frac{3}{2}}} - \dfrac{(1 - \mu) x_2}{\Big( x_2^2 + x_3^2 + (x_1 + \mu)^2 \Big)^{\frac{3}{2}}} \\ \dot{u_3} & = & - \dfrac{\mu x_3}{\Big( x_2^2 + x_3^2 + (x_1 + \mu - 1)^2 \Big)^{\frac{3}{2}}} - \dfrac{(1 - \mu) x_3}{\Big( x_2^2 + x_3^2 + (x_1 + \mu)^2 \Big)^{\frac{3}{2}}} \\ \end{align}\]

Equilateral Lagrange Points

\[L_{4,5} = \Bigg(\dfrac{1}{2} - \mu, \pm \dfrac{\sqrt{3}}{2}, 0 \Bigg)\]

Collinear Lagrange Points

\[\begin{align} L_1: & -1.0 < x_1 < 1.0 \\ L_2: & \quad 1.0 < x_1 < 1.25 \\ L_3: & -1.25 < x_1 < -1.0 \\ \end{align}\] \[0 = x_1 - \dfrac{\mu (x_1 + \mu - 1)}{\Big\vert x_1 + \mu - 1 \Big\vert^3} - \dfrac{(1 - \mu)(x_1 + \mu)}{\Big\vert x_1 + \mu \Big\vert^3}\]

The Jacobi constant

The pseudo-potential function in the rotating frame is given by

\[U = - \dfrac{\mu}{\sqrt{x_2^2 + x_3^2 + (x_1 + \mu - 1)^2}} - \dfrac{1 - \mu}{\sqrt{x_2^2 + x_3^2 + (x_1 + \mu)^2}} - \dfrac{1}{2}\Bigg[ \mu \bigg( x_2^2 + x_3^2 + (x_1 + \mu - 1)^2 \bigg) + (1 - \mu) \bigg( x_2^2 + x_3^2 + (x_1 + \mu)^2 \bigg) \Bigg]\]

The value

\[J = \dfrac{1}{2} \Big[ u_1^2 + u_2^2 + u_3^2 \Big] + U\]

is called the Jacobi constant, and represents the total energy of the tertiary mass relative to the rotating reference frame.

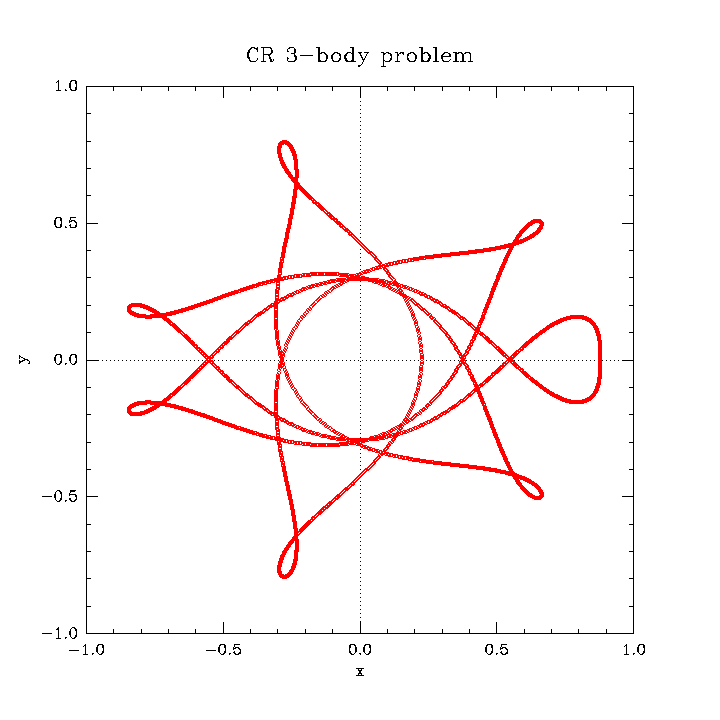
Pseudo-periodic orbit

Initial conditions for Earth-Moon like system $\mu = 1/81.45$

\[\mathbf{x}_0 = (0.87978, 0, 0) \quad \mathbf{u}_0 = (0, -0.3797, 0) \quad T = 19.14045706162071\]