Sandbox

Kepler problem

Numerical integration

Equations of motion

Lagrangian

\[\mathcal{L} = \dfrac{1}{2}\big( \dot{x}_1^2 + \dot{x}_2^2 \big) + \dfrac{1}{\sqrt{ x_1^2 + x_2^2}}\]

Equations of motion

\[\begin{cases} & \ddot{x}_1 & = & - \dfrac{x_1}{\big( x_1^2 + x_2^2 \big)^{\frac{3}{2}}} \\ & \ddot{x}_2 & = & - \dfrac{x_2}{\big( x_1^2 + x_2^2 \big)^{\frac{3}{2}}} \end{cases}\]

Constants of motion

\[\begin{align} \mathcal{E}_0 & = & \dfrac{1}{2}\big( \dot{x}_1^2 + \dot{x}_2^2 \big) - \dfrac{1}{\sqrt{ x_1^2 + x_2^2}} \\ L_0 & = & x_1 \dot{x}_2 - x_2 \dot{x_1} \end{align}\]

Bounded orbits

Elliptical orbit with eccentricity $\epsilon = 0 \ldots 1$ and period $T = 2\pi$.

Initial conditions

\[x_1 = 1 - \epsilon; \quad x_2 = 0; \quad \dot{x}_1 = 0; \quad \dot{x}_2 = \sqrt{\dfrac{1 + \epsilon}{1 - \epsilon}}\]

For $\epsilon = 0.6$ and $N = 120$

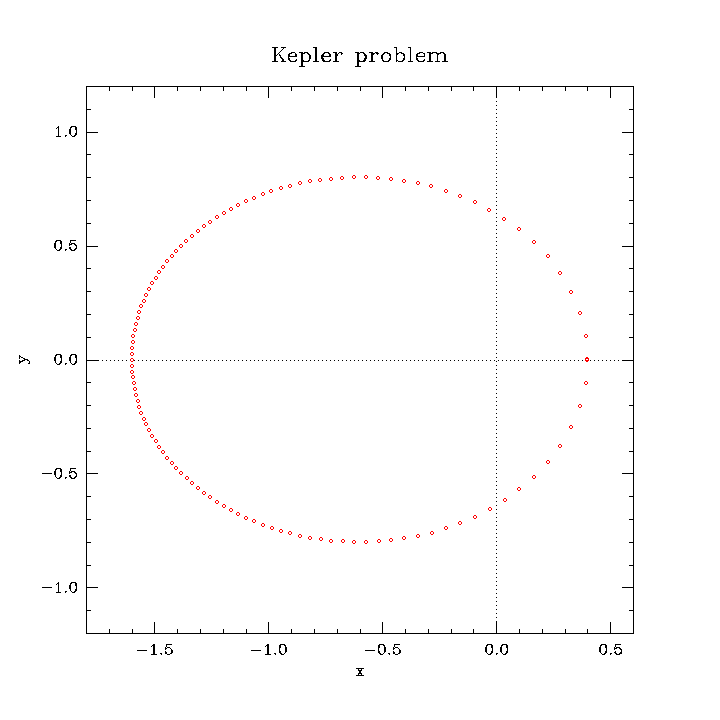
plotutils ode

ODE description

# Kepler problem

eps = 0.6

x1' = u1
x2' = u2
u1' = -x1/(sqrt(x1^2 + x2^2))^3
u2' = -x2/(sqrt(x1^2 + x2^2))^3

x1 = 1 - eps
x2 = 0
u1 = 0
u2 = sqrt((1 + eps)/(1 - eps))

E0 = u1^2/2 + u2^2/2 - 1/sqrt(x1^2 + y2^2)

print x1, u1, x2, u2, E0
step 0, 8*atan(1), 8*atan(1)/120