Sandbox

Lorenz system

Lorenz equations

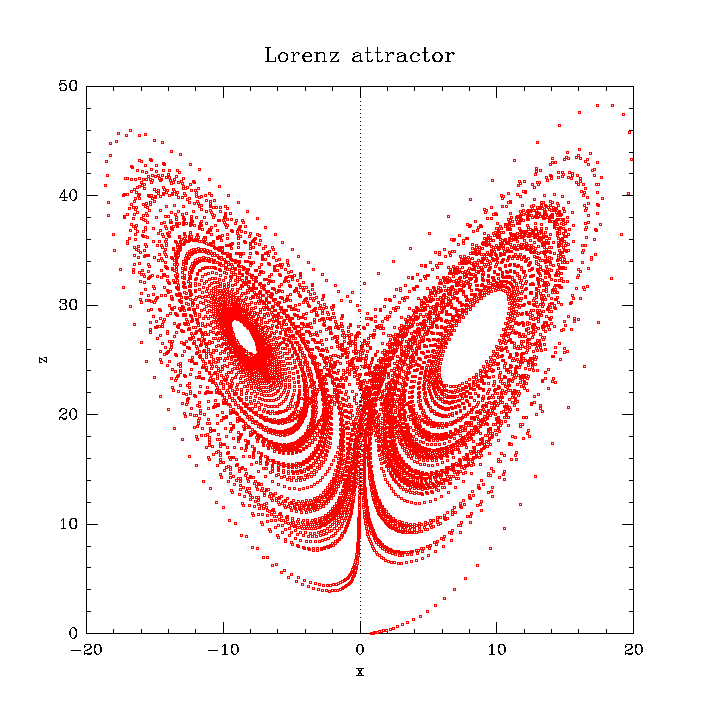
The Lorenz attractor arises in a simplified system of equations describing the two-dimensional flow of fluid of uniform depth.

\[\begin{align} \dot{x} & = & \sigma (y - x) \\ \dot{y} & = & x (\rho - z) - y \\ \dot{z} & = & x y - \beta z \end{align}\]

The parameters $\sigma$, $\rho$, and $\beta$ are positive.

Critical points

If $\rho < 1$ then there is only one equilibrium point $(0, 0, 0)$. For $\rho > 1$ two additional critical points appear at

\[\begin{align} \Big( \sqrt{\beta (\rho - 1)}, \sqrt{\beta (\rho - 1)}, \rho - 1 \Big) \\ \Big( -\sqrt{\beta (\rho - 1)}, -\sqrt{\beta (\rho - 1)}, \rho - 1 \Big) \end{align}\]

They are stable if

\[\rho < \sigma \dfrac{\sigma + \beta + 3}{\sigma - \beta - 1} \qquad \sigma > \beta + 1\]

Chaotic behavior

The system exhibits chaotic behavior for values near $\sigma = 10$, $\rho = 28$, $\beta = \frac{8}{3}$.

For initial conditions $(1, 0, 0)$