Sandbox

Mathematical pendulum

Equations of motion

Hamiltonian

\[\mathcal{H} = \dfrac{1}{2}p^2 + 2\sin^2\dfrac{\theta}{2}\]

Equations of motion

\[\begin{cases} &\dot{\theta} & = & p \\ &\dot{p} & = & -\sin\theta \end{cases}\]

Solultions can be expressed via Jacobi elliptic functions. Select initial conditions so that $\theta(t = 0) = 0$

Librations

Case $\mathcal{E} < 2$. Assign $k^2 = \dfrac{1}{2}\mathcal{E}$

\[\begin{align} \theta & = & 2 \arcsin\big( k \cdot \mathrm{sn}(t; k) \big) \\ p & = & 2k \cdot \mathrm{cn}(t; k) \end{align}\]

Period of librations $T = 4\mathrm{K}(k)$

Rotations

Case $\mathcal{E} > 2$. Assign $k^2 = 2\mathcal{E}^{-1}$

\[\begin{align} \theta & = & 2 \cdot \mathrm{am}\bigg( \dfrac{t}{k}; k \bigg) \\ p & = & \dfrac{2}{k} \mathrm{dn}\bigg( \dfrac{t}{k}; k \bigg) \end{align}\]

Period of rotations $T = 2k \cdot \mathrm{K}(k)$

Numerical solution

For initial conditions

\[\theta=\dfrac{\pi}{2}, \quad p = 0\]

Period $T = 4\mathrm{K}\big( \frac{1}{2} \big) \approx 7.4163$

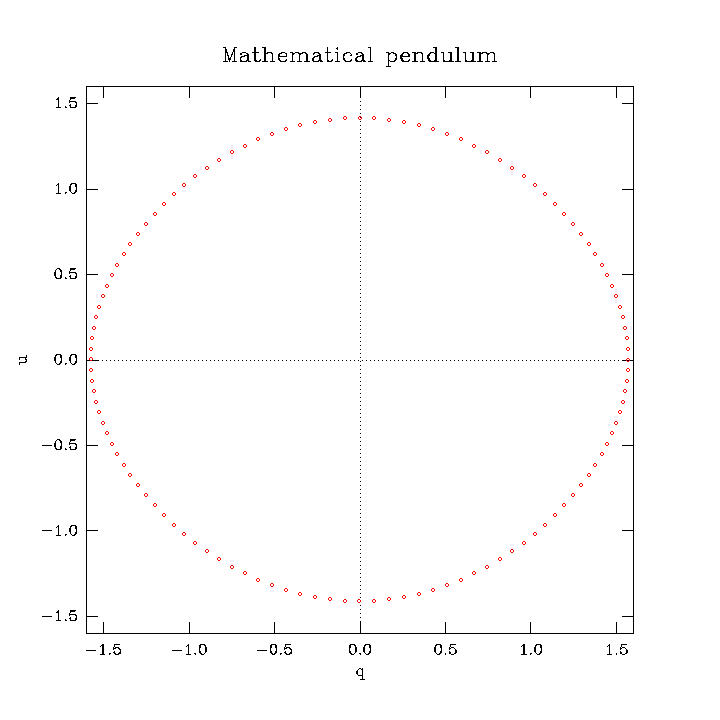
plotutils ode

ODE description

# Mathematical pendulum

q' = u
u' = -sin(q)

q = 3*atan(1/sqrt(3))
u = 0

E0 = u^2/2 + 1 - cos(q)
#T = 8*atan(1)*(1 + (1/4)*(1-1/4))

print q, u, E0
step 0, 7.4163, 7.4163/120